ВСЕ РАЗДЕЛЫ
- Неопределенность и риск
- Страховые портфели
- Цена страхования
- Введение в теорию полезности
- Характеризация отношения к риску
- Простейший процесс риска
- Классический процессриска
- Агрегированный процесс риска
- Время жизни процессов риска
- Финансовый кризис 2008
НОВОСТИ ФИНАНСОВ
| Опубликовал: Administrator | |
|
12.07.2008 4.3 Теорема о существовании функции полезности 4.3.1 Система аксиом Введем на Pоперацию смеси распределений: для произвольных и числа смесью Pi и Рг назовем распределение задаваемое соотношением Будем предполагать выполненной следующую систему аксиом. Приведенные аксиомы можно трактовать, как требования наличия у отношения предпочтения некоторой регулярности, "правильности". 4.3.2 Теорема существования Прежде чем формулировать основную теорему, докажем несколько лемм. Лемма 4.1 Пусть выполнены аксиомы Тогдасуществует единственная постоянная такая, что Доказательство. Заметим, что если то соотношение (28) выполняется при единственном значении а = 1 (см. упражнение 4.6). Аналогично, если то (28) выполняется только при а = 0 (см. упражнение 4.7). Пусть теперь Тогда по аксиоме А4 существует такое, что выполнено Предположим, что такое а.- неединственное, и существует для которого Положим для определенности Тогда и Поскольку по аксиоме A3 и (31) получаем Отсюда с использованием аксиомы A3 и (32) получаем: Это соотношение противоречит (29),(30), так что постоянная а\, для которой выполнено (29) - единственна Лемма 4.2 Если выполнены аксиомы таковы, что то (монотонность операции смешивания) Доказательство. Пусть, напротив, Тогда, по аксиомам A3, А4 имеем: 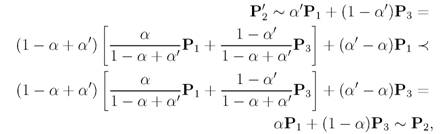 так что - противоречие. Теорема 4.3 Если выполнены аксиомы то существует вещественнознач функция U: называемая функцией полезности, и такая, что для произвольных соотношение эквивалентно - случайные элементы, задающие распределения соответственно. Более того, функция Uединственна с точностью до положительного аффинного преобразования. Моделирование финансовых рисков Замечание 4.2 Теорема 4-3 позволяет в качестве средства для сравнения рисков по предпочтительности использовать их ожидаемую полезность Доказательство теоремы 4.3 проведем в предположении конечности множества результатов: При этом каждое распределение можно представить вектором так что Рассмотрим распределения Без ограничения общности можем считать, что Покажем теперь, что так определенная функция Uобладает свойством (36). Для произвольного распределения Р = (рг, ...,Pn) £ V, как нетрудно заметить PNУ Р У Pi (см. упражнение 4.9), так что мы можем задать а(Р) как (однозначно определенную) постоянную из [0,1], для которой или, что эквивалентно, 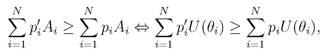 и (36) доказано. Осталось показать, что Uопределено единственным образом с точностью до положительного аффинного преобразования. Пусть U* - другая функция полезности, удовлетворяющая (36). Обозначим А* = U*(0i), г = 1,..., N из (36) и (39) имеем: откуда так что Таким образом, U* действительно является положительным аффинным преобразованием от U. о Упражнение 4.6 Доказать, что в условиях леммы 4-1 условие влечет выполнение (28) при единственном значении а = 1. Упражнение 4.7 Доказать, что в условиях леммы 4-1 условие влечет выполнение (28) при единственном значении а = 0. Упражнение 4.8 Доказать, что если в условиях теоремы 4-3 то ее утверждение справедливо. Упражнение 4.9 Доказать, что если в условиях теоремы 4-3 справедливо (37), то для произвольного распределения имеет место 4.4 Решения Введем теперь в рассмотрение активного индивидуума. Пусть Л обозначает множество его действий (решений), и поведение системы в целом описывается функцией измеримой относительно и при каждом фиксированном а £ А (т.е. так что если индивидуум принял решение а среда оказалась в (случайном) состоянии то результатом действия а будет Так, например, решением а может служить структура инвестиционного портфеля, состоянием среды - доходности ценных бумаг, входящих в портфель, а результатом доходность портфеля в целом.
|
|