В параграфах 6-8 получены уравнения для вероятности разорения. Представляет интерес также и момент разорения. В настоящем параграфе изучим среднее время жизни процессов риска.

9.1 Простейший процесс риска
Рассмотрим простейший процесс риска (53):

где

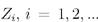
- независимые одинаково распределенные случайные величины, принимающие значение 1 с вероятностью p и значение -1с вероятностью

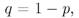
и обозначим

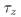
момент окончания игры (разорения одного из игроков) при условии, что первый игрок имел начальный капитал

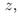
а второй:


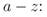
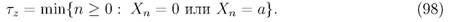
Как мы помним, на бесконечном горизонте времени разорение одного из игроков
наступает с вероятностью 1, так что

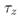
является собственной случайной величиной.
Обозначим m(z) = Etzее среднее значение, и поставим задачу вычисления этой величины. Из формулы полной вероятности для математических ожиданий нетрудно получить уравнение для m(z) вида m(z) = 1 + pm(z+ 1) + qm(z— 1), откуда

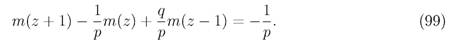
Характеристическое уравнение для (99) имеет корни Ai = 1; А2 = q/p= у. Рассмотрим сначала случай некратных корней у ф 1 (р ф 1/2)- Тогда частное решение неоднородного уравнения (99) имеет вид тщ{г) = , z_x), так что его общее решение запишется в форме

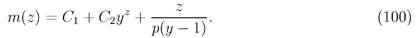
Произвольные постоянные С\,Сч можно определить из краевых условий гп(0) = тп(а) = 0, которые дают

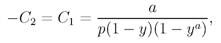
так что решение уравнения (99) есть

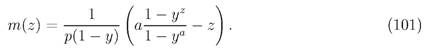
В случае кратных корней у = 1 (р = 1/2) общее решение уравнения (99) имеет вид С\ + C2Z+ mo(z), где частное решение mo(z) легко находится в классе квадратичных функций и равно mo(z) = —z2, так что искомое решение после определения постоянных из краевых условий записывается в форме

Интересно отметить, что решение (102) может быть получено предельным переходом из (101) с помощью двукратного применения правила Лопиталя.
Рассмотрим, наконец, игру с бесконечно богатым противником (а —> сю). При у < 1 из (101), видно, что среднее время жизни неограниченно увеличивается. Этот эффект связан с тем, что при у < 1 имеем р > 1/2, и даже в игре с бесконечно богатым противником первый игрок разоряется с вероятностью, меньшей 1, то есть с положительной вероятностью время жизни процесса бесконечно.
При у = 1 из (102) также вытекает m(z) —> сю при а —> сю. Отсюда вытекает, что хотя в этом случае (р = 1/2) первый игрок и разоряется с вероятностью 1 в игре с бесконечно богатым противником, однако среднее время ожидания разорения бесконечно велико.
При у > 1 (р < 1/2) из (101) следует, что ожидаемое время до разорения в игре с бесконечно богатым противником есть

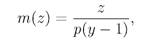
и линейно возрастает вместе с z.